In this section we describe the basic features of zero dynamics. The zero dynamics can be seen as the remaining dynamics of a system when we steer the output to be identically zero. We will give a brief account for some definitions and results which can be found in e.g. Isidori [5]. First we interpret the zero dynamics of a single-input single-output (SISO) system, especially in the linear case, both in the frequency domain and in the time domain and then we extend the concept to multi-input multi-output (MIMO) systems.
Definition 2.1: The single-input single-output nonlinear system
![]()
![]()
is said to have relative degree ![]() at a point
at a point ![]() if
if
\begin{itemize}
\item[i] ![]() for all
for all ![]() in a neighborhood of
in a neighborhood of ![]() and all
and all ![]() ,
,
\item[ii] ![]() ,
,
where ![]() is the so-called derivative of
is the so-called derivative of ![]() along
along ![]() , defined by
, defined by
![]()
\end{itemize}
The derivative of order ![]() ,
, ![]() , satisfies the recursion
, satisfies the recursion
![]()
![]()
Similarly, we have
![]()
For the linear system
(1) ![]()
we have
![]()
and therefore
![]()
Thus, the integer ![]() is characterized by the conditions
is characterized by the conditions
(2) ![]()
It can be shown that the integer ![]() satisfying these conditions is exactly equal to the difference between the degree of the denominator polynomial and the degree of the numerator polynomial,
satisfying these conditions is exactly equal to the difference between the degree of the denominator polynomial and the degree of the numerator polynomial,
![]()
that is, the number of poles and the number of zeros, respectively, of the transfer function
![]()
of the linear system (1).
In particular, any linear system with ![]() -dimensional state-space and relative degree
-dimensional state-space and relative degree ![]() , which is strictly less than
, which is strictly less than ![]() , as zeros in its transfer function. If, on the contrary,
, as zeros in its transfer function. If, on the contrary, ![]() , the transfer function has no zeros.
, the transfer function has no zeros.
We can also interpret the relative degree in the time domain as follows. Consider the SISO system (??) and assume that it is in state ![]() at time
at time ![]() . Calculating the value of the output
. Calculating the value of the output ![]() and of its derivatives
and of its derivatives ![]() ,
, ![]() , at
, at ![]() , using definition 2.1, we obtain
, using definition 2.1, we obtain
(3) ![]()
If the relative degree ![]() is larger than 1 for all
is larger than 1 for all ![]() in a neighborhood of
in a neighborhood of ![]() , we have
, we have ![]() and therefore
and therefore
![]()
The derivative of second order is
![]()
and if the relative degree is larger than 2 for all ![]() in a neighborhood of
in a neighborhood of ![]() , we have
, we have ![]() , so that
, so that
![]()
In the ![]() th step we have
th step we have
(4) ![]()
Thus, the relative degree ![]() is exactly equal to the number of times the output
is exactly equal to the number of times the output ![]() has to be differentiated at
has to be differentiated at ![]() in order to have the value
in order to have the value ![]() of the input explicitly appearing in the expression for the differentiated output. If
of the input explicitly appearing in the expression for the differentiated output. If
![]()
for all ![]() and all
and all ![]() in a neighborhood of
in a neighborhood of ![]() (in which case no relative degree can be defined there), then the output is unaffected by the input for
(in which case no relative degree can be defined there), then the output is unaffected by the input for ![]() close to
close to ![]() and
and
![Rendered by QuickLaTeX.com \[y(t)=\sum_{k=0}^{\infty} L_f^kh(x^0)\frac {(t-t_0)^k}{k!}\]](https://www.mathgallery.com/wp-content/ql-cache/quicklatex.com-53f3aa55b7efa762d3f3939105d57c88_l3.png)
is a function depending only on the initial state and not on the input.
Now we consider the so-called normal form of a system, which we obtain by making a special coordinate trans-formation. In this form, it is easy to see some of the properties of solutions of certain control problems. From Isidori [5, pp.149-150], we state the following
Proposition 2.1: Suppose that a SISO system has relative degree ![]() at a point
at a point ![]() , where
, where ![]() . Set
. Set
(5) 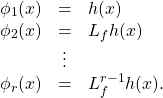
If ![]() is strictly less than
is strictly less than ![]() , it is always possible to find
, it is always possible to find ![]() more functions
more functions
![]()
such that the mapping
(6) 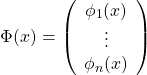
has a Jacobian matrix which is nonsingular at ![]() and therefore can be used as a coordinate transformation in a neighborhood of
and therefore can be used as a coordinate transformation in a neighborhood of ![]() . The value at
. The value at ![]() of these additional functions can be fixed arbitrarily. Moreover, it is always possible to choose
of these additional functions can be fixed arbitrarily. Moreover, it is always possible to choose ![]() in such a way that
in such a way that
![]()
for all ![]() and all
and all ![]() in a neighborhood of
in a neighborhood of ![]() .
.
Now, letting
![]()
we obtain for ![]()
(7) 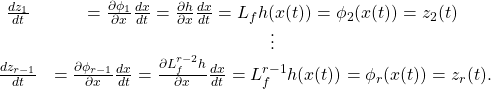
For ![]() we obtain
we obtain
(8) ![]()
We substitute
![]()
into the right-hand side of (8) and let
(9) ![]()
so that we have
(10) ![]()
where, at the point ![]() ,
, ![]() by definition. Thus, the coefficient
by definition. Thus, the coefficient ![]() is nonzero for all
is nonzero for all ![]() in a neighborhood of
in a neighborhood of ![]() . Now we choose
. Now we choose ![]() in such a way that
in such a way that
![]()
so that
(11) ![]()
Setting
![]()
for all ![]() , we can write
, we can write
(12) ![]()
Since ![]() , we immediately get the output
, we immediately get the output ![]() in the new coordinates. Now we define the vectors
in the new coordinates. Now we define the vectors
(13) 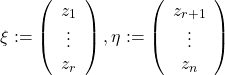
so that the normal form can be written
(14) 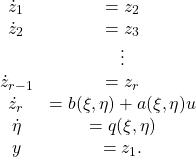
Note that it is always possible to choose arbitrarily the value at ![]() of the last
of the last ![]() coordinates. Therefore, without loss of generality, we can assume that
coordinates. Therefore, without loss of generality, we can assume that ![]() and
and ![]() at
at ![]() . In order to have
. In order to have ![]() for all
for all ![]() we must have
we must have
![]()
that is, ![]() for all
for all ![]() . Furthermore, the input
. Furthermore, the input ![]() must satisfy
must satisfy
![]()
where ![]() if
if ![]() is close to
is close to ![]() . The remaining dynamics
. The remaining dynamics
![]()
are called the zero dynamics of the system.
In order to interpret the concept of zero dynamics in the frequency domain and in the time domain, we consider a SISO linear system with relative degree ![]() and transfer function
and transfer function
(15) ![]()
Suppose that the polynomials ![]() and
and ![]() are coprime, i.e. the polynomials do not have any common zeros, and consider the minimal realization
are coprime, i.e. the polynomials do not have any common zeros, and consider the minimal realization
(16) ![]()
(17) 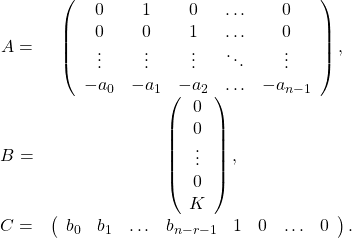
In the frequency domain we consider the equation
![]()
where ![]() and
and ![]() are the Laplace transforms of the output
are the Laplace transforms of the output ![]() and the input
and the input ![]() , respectively. Thus, we have
, respectively. Thus, we have
![]()
Now we multiply the numerator and denumerator of the transfer function by an arbitrary nonzero variable ![]() , so that
, so that
![]()
and we observe that ![]() exactly when
exactly when ![]() . Taking the inverse Laplace transform of
. Taking the inverse Laplace transform of
![]()
and defining the new coordinates according to
(18) 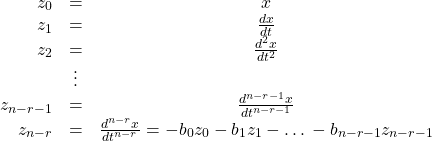
we have
(19) 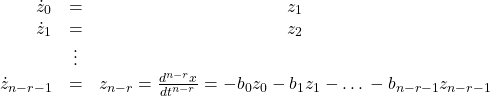
and we can write the system as
![]()
(20) 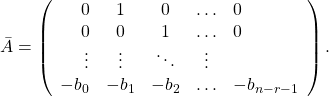
The eigenvalues of (20) are exactly the zeros of the transfer function (15). To see this, we transform ![]() to triangular form, i.e. the matrix
to triangular form, i.e. the matrix
![Rendered by QuickLaTeX.com \[\left(\begin{array}{ccccc}s& -1& 0& \ldots & 0\\0& s& -1& \ldots & 0\\\vdots & \vdots & \vdots &\ddots & \vdots \\b_0& b_1& b_2& \ldots & s+b_{n-r-1}\end{array}\right)\]](https://www.mathgallery.com/wp-content/ql-cache/quicklatex.com-c4a2b8f2c3dab9261b43beded67d8938_l3.png)
is transformed to
![Rendered by QuickLaTeX.com \[\left(\begin{array}{ccccc}s& -1& 0& \ldots & 0\\0& s& -1& \ldots & 0\\\vdots & \vdots & \vdots &\ddots & \vdots \\0& 0& 0& \ldots & \alpha \end{array}\right),\]](https://www.mathgallery.com/wp-content/ql-cache/quicklatex.com-fa1e4cc1000e50dda629560b34dd7cfc_l3.png)
where
![]()
from which we see that the determinant
![]()
is exactly the numerator polynomial ![]() of the transfer function (15). This is the reason for the name zero dynamics; in fact, zero dynamics can be seen as a generalization of the transmission zeros of linear systems, as we show in the end of this section.
of the transfer function (15). This is the reason for the name zero dynamics; in fact, zero dynamics can be seen as a generalization of the transmission zeros of linear systems, as we show in the end of this section.
Now we consider the time domain representation (16) of a SISO linear system with
matrices given by (17) and calculate its normal form. For the first ![]() coordinates we have to take
coordinates we have to take
(21) 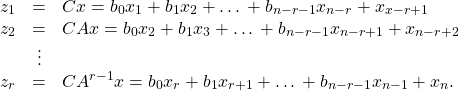
The remaining ![]() coordinates are chosen so that the conditions of proposition 2.1 are satisfied. We can, for example, choose
coordinates are chosen so that the conditions of proposition 2.1 are satisfied. We can, for example, choose
(22) 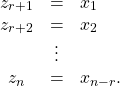
This is an admissible choice since the corresponding transformation matrix ![]() has a nonsingular Jacobian
has a nonsingular Jacobian ![]() . Thus, we have
. Thus, we have
(23) 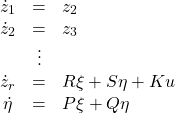
where ![]() and
and ![]() are row vectors,
are row vectors, ![]() and
and ![]() matrices of suitable dimensions and
matrices of suitable dimensions and ![]() and
and ![]() are defined as in (13). The zero dynamics of this system are
are defined as in (13). The zero dynamics of this system are
![]()
According to our choice of the last ![]() coordinates (i.e. the elements of
coordinates (i.e. the elements of ![]() ), we have
), we have
(24) 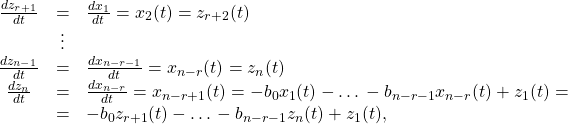
where ![]() since the output is zero. We see that
since the output is zero. We see that ![]() , where
, where ![]() is given by (20).
is given by (20).
We can quite easily extend the concepts of relative degree and zero dynamics to the multi-input multi-output (MIMO) case. Consider the multivariable nonlinear system with the same number ![]() of inputs and outputs
of inputs and outputs
(25) 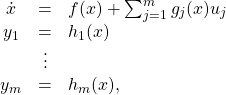
in which ![]() are smooth vector fields, and
are smooth vector fields, and ![]() are smooth functions, defined on an open set of
are smooth functions, defined on an open set of ![]() .
.
Definition 2.2: A multivariable nonlinear system of the form (25) is said to have a (vector) relative degree ![]() at a point
at a point ![]() if
if
\begin{itemize}
\item[(i)] ![]() for all
for all ![]() ,
, ![]() ,
, ![]() , and for all
, and for all ![]()
in a neighborhood of ![]() .
.
\item[(ii)] the ![]() matrix
matrix
(26) 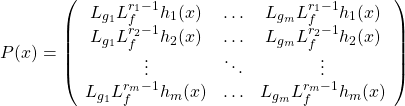
is nonsingular at ![]() .
.
Note that each integer ![]() is associated with the
is associated with the ![]() th output of the system. Furthermore, in a neighborhood of
th output of the system. Furthermore, in a neighborhood of ![]() , the row vector
, the row vector
![]()
is zero for all ![]() and, for
and, for ![]() , this vector is nonzero (i.e. has at least one nonzero element). Thus, for each
, this vector is nonzero (i.e. has at least one nonzero element). Thus, for each ![]() there is at least one
there is at least one ![]() such that the SISO system having output
such that the SISO system having output ![]() and input
and input ![]() has exactly relative degree
has exactly relative degree ![]() at
at ![]() and, for any other possible choice of
and, for any other possible choice of ![]() , the corresponding relative degree at
, the corresponding relative degree at ![]() – if any – is necessarily higher than or equal to
– if any – is necessarily higher than or equal to ![]() . Similarly to the SISO case,
. Similarly to the SISO case, ![]() is the number of times
is the number of times ![]() , the
, the ![]() th output vector, has to be differentiated at
th output vector, has to be differentiated at ![]() in order to have at least one component of the input vector
in order to have at least one component of the input vector ![]() explicitly appearing.
explicitly appearing.
The normal form of a multi-input multi-output system can be written
(27) 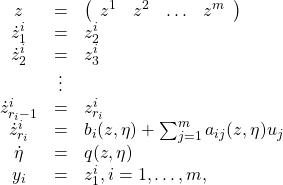
where
(28) ![]()
The the zero dynamics of (27) can be written
(29) ![]()
However, instead of considering the conditions under which a transformation exists which transforms a system to its normal form, we will state a more general definition which is independent of the relative degree.
Definition 2.3: Consider the system (25) with equal number ![]() of inputs and outputs. Let the state
of inputs and outputs. Let the state ![]() be defined on an open set
be defined on an open set ![]() of
of ![]() . Suppose that
. Suppose that ![]() ,
, ![]() ,
, ![]() and that there exists a smooth connected submanifold
and that there exists a smooth connected submanifold
![]() of
of ![]() which contains
which contains ![]() and satisfies\begin{itemize}
and satisfies\begin{itemize}
\item[(i)] ![]() ,
,
\item[(ii)] at each point ![]() there exists a unique
there exists a unique ![]() such that
such that ![]() is tangent to
is tangent to ![]() .\item[(iii)]
.\item[(iii)] ![]() is maximal with respect to (i) and (ii).\end{itemize}
is maximal with respect to (i) and (ii).\end{itemize}
Then ![]() is called the zero dynamics manifold and
is called the zero dynamics manifold and
![]()
is the zero dynamics of (25).
Even for multivariable systems we can interpret the zero dynamics as a nonlinear analogue of the “zeros” of a linear system. Consider the linear system
(30) ![]()
In the linear case, the conditions of definition 2.3 give the problem of finding the maximal controlled invariant subspace ![]() such that
such that ![]() . Clearly, we must have
. Clearly, we must have
![]()
We are looking for a state feedback ![]() such that
such that ![]() is tangent to
is tangent to ![]() , i.e.
, i.e. ![]() is in
is in ![]() for all
for all ![]() . This is equivalent to the condition
. This is equivalent to the condition
![]()
Thus, ![]() is just the largest controlled invariant subspace of the system (30). Now, making the additional assumptions
is just the largest controlled invariant subspace of the system (30). Now, making the additional assumptions
![]()
a unique control law ![]() exists and we see that the largest controllability subspace
exists and we see that the largest controllability subspace ![]() from the definition
from the definition
![]()
(31) ![]()
identifies a linear dynamical system, defined on ![]() , whose dynamics are by definition the zero dynamics of the original system. Furthermore, the eigenvalues of (31) coincide with the so-called transmission zeros of the system.
, whose dynamics are by definition the zero dynamics of the original system. Furthermore, the eigenvalues of (31) coincide with the so-called transmission zeros of the system.
To see this, consider the following proposition, see Wonham [2, pp. 111-112], from which the definition of transmission zeros readily follows.
Proposition 2.2: Consider the system (30). Let ![]() be a map
be a map ![]() such that
such that ![]() , where
, where ![]() is the largest controlled invariant subspace, and let
is the largest controlled invariant subspace, and let ![]() be the largest controllability subspace. Then
be the largest controllability subspace. Then
![]()
where
![]()
is freely assignable by suitable choice of ![]() , and
, and
![]()
is fixed for all ![]() . The fixed spectrum
. The fixed spectrum ![]() is called the set of transmission zeros of the linear system.
is called the set of transmission zeros of the linear system.
If the numbers of inputs and outputs are not equal, we can drop the assumption that ![]() and simply
and simply
redefine the zero dynamics to be the dynamics of the system (30) restricted to the subspace
(32) ![]()
which is the definition we will use in the sequel.
Similarly to the SISO case, it can be shown that a MIMO system which has a relative degree ![]() at the point
at the point ![]() where
where ![]() can be transformed into a fully linear and controllable system by means of feedback and transformation of coordinates. Such a system has a 0-dimensional zero dynamics manifold, i.e. has no zero dynamics, see Isidori [5, p. 382].
can be transformed into a fully linear and controllable system by means of feedback and transformation of coordinates. Such a system has a 0-dimensional zero dynamics manifold, i.e. has no zero dynamics, see Isidori [5, p. 382].
We conclude this section with one more definition.
Definition 2.4: If the eigenvalues of the zero dynamics (32) lie off the imaginary axis, i.e. if
![]()
then the zero dynamics are called hyperbolic.
