A strong control action can force a system to have fast and slow transients, i.e. to behave like a singularly perturbated system. In feedback systems, the strong control action is achieved by high feedback gain, e.g. as a result of a cheap optimal control problem. We give a brief account for the methods to be used in our analysis of the cheap control regulator. Basic results and singular pertubation techniques applied to different problems can be found in e.g. Kokotovič et al. [6].
Consider the singular perturbation model of finite-dimensional dynamic systems
(1) ![]()
where ![]() and
and ![]() are assumed to be sufficiently many times continuously differentiable. When we set
are assumed to be sufficiently many times continuously differentiable. When we set ![]() , the dimension of the state-space of (1) is reduced from
, the dimension of the state-space of (1) is reduced from ![]() to
to ![]() as the second equation degenerates into the algebraic (or transcendental) equation
as the second equation degenerates into the algebraic (or transcendental) equation
(2) ![]()
where ![]() and
and ![]() belong to a system with
belong to a system with ![]() . We say that the model (1) is in standard form if and only if the following assumption is satisfied.
. We say that the model (1) is in standard form if and only if the following assumption is satisfied.
Assumption 2.1: In a domain of interest, the equation (2) has ![]() distinct real roots
distinct real roots
(3) ![]()
This assumption ensures that a well-defined ![]() -dimensional reduced model will correspond to each root (3). Substituting (3) into the first equation of (1) gives the
-dimensional reduced model will correspond to each root (3). Substituting (3) into the first equation of (1) gives the ![]() th reduced (quasi-steady-state) model
th reduced (quasi-steady-state) model
(4) ![]()
where we use the same initial condition for ![]() as for
as for ![]() .
.
Singular perturbation cause a multi-time-scale behavior of dynamic systems characterized by slow and fast transients in the system response. The slow response is approximated by (4) while the discrepancy between the response of the reduced model (4) and the full model (1) is the fast transient. In removing the variable ![]() from the original system (1) and replacing it by its quasi-steady-state
from the original system (1) and replacing it by its quasi-steady-state ![]() , we have to consider the fact that
, we have to consider the fact that ![]() is not free to start at
is not free to start at ![]() from
from ![]() , the initial condition for
, the initial condition for ![]() . There may be a large discrepancy between the initial condition
. There may be a large discrepancy between the initial condition ![]() and the initial value of
and the initial value of ![]() ,
,
![]()
Thus, ![]() cannot be a uniform approximation of
cannot be a uniform approximation of ![]() . The best approximation we can obtain is that
. The best approximation we can obtain is that
(5) ![]()
will hold on an interval excluding ![]() , i.e. for all
, i.e. for all ![]() , where
, where ![]() . However, we can constrain the quasi-steady-state
. However, we can constrain the quasi-steady-state ![]() to start from the prescribed initial condition
to start from the prescribed initial condition ![]() , and therefore the approximation of
, and therefore the approximation of ![]() by
by ![]() may be uniform. In other words,
may be uniform. In other words,
(6) ![]()
will hold on an interval including ![]() , i.e. for all
, i.e. for all ![]() on which
on which ![]() exists. The approximation (5) establishes that during an initial “boundary layer” interval
exists. The approximation (5) establishes that during an initial “boundary layer” interval ![]() , the original variable
, the original variable ![]() approaches
approaches ![]() and then, during
and then, during ![]() , remains close to
, remains close to ![]() . The speed of
. The speed of ![]() can be large,
can be large, ![]() . In fact, having set
. In fact, having set ![]() equal to zero in (1), we have made the transient instantaneous whenever
equal to zero in (1), we have made the transient instantaneous whenever![]() . To see whether
. To see whether ![]() will escape to infinity during this transient or converge to its quasi-steady-state, we analyze
will escape to infinity during this transient or converge to its quasi-steady-state, we analyze ![]() , which may be finite, even when
, which may be finite, even when ![]() tends to zero and
tends to zero and ![]() tends to infinity. We change coordinates according to
tends to infinity. We change coordinates according to
![]()
so that
![]()
and use ![]() as the initial value at
as the initial value at ![]() . We then have the new time variable
. We then have the new time variable
![]()
so that, if ![]() tends to zero,
tends to zero, ![]() tends to infinity even for fixed
tends to infinity even for fixed ![]() only slightly larger than
only slightly larger than ![]() . On the other hand, while
. On the other hand, while ![]() and
and ![]() almost instantaneously change,
almost instantaneously change, ![]() remains very near its initial value
remains very near its initial value ![]() . Consider the so-called boundary layer correction
. Consider the so-called boundary layer correction ![]() satisfying the boundary layer system
satisfying the boundary layer system
(7) ![]()
with the initial condition ![]() , where
, where ![]() and
and ![]() are fixed parameters. The solution
are fixed parameters. The solution ![]() of this initial value problem is used as a boundary layer correction of (5) for a possibly uniform approximation of
of this initial value problem is used as a boundary layer correction of (5) for a possibly uniform approximation of ![]() :
:
(8) ![]()
Clearly, ![]() is the slow transient of
is the slow transient of ![]() and
and ![]() is the fast transient of
is the fast transient of ![]() . For the corrected approximation (8) to converge, after a short period, to the slow approximation (5), the
. For the corrected approximation (8) to converge, after a short period, to the slow approximation (5), the
correction term ![]() must decay as
must decay as ![]() to an
to an ![]() quantity. Note that in the slow time scale
quantity. Note that in the slow time scale ![]() this decay is rapid since
this decay is rapid since
![]()
The stability properties of the boundary layer system (7), which are crucial for the approximations (5), (6) and (8) to hold can be stated as two assumptions.
Assumption 2.2: The equilibrium ![]() of (7) is assyptotically stable uniformly in
of (7) is assyptotically stable uniformly in ![]() and
and ![]() , and
, and ![]() belongs to its domain of attraction, so
belongs to its domain of attraction, so ![]() exists for
exists for ![]() .
.
If this assumption is satisfied, then
![]()
uniformly in ![]() ,
, ![]() . Thus,
. Thus, ![]() will come close to its quasi-steady-state
will come close to its quasi-steady-state ![]() at some time
at some time ![]() . To ensure that
. To ensure that ![]() stays close to
stays close to ![]() , we think as if any instant
, we think as if any instant ![]() can be the initial instant, and make the following assumption about the linearization of (7).
can be the initial instant, and make the following assumption about the linearization of (7).
Assumption 2.3: The eigenvalues of ![]() evaluated, for
evaluated, for ![]() , along
, along ![]() ,
, ![]() , have real parts smaller than a fixed negative number, i.e.
, have real parts smaller than a fixed negative number, i.e.
(9) ![]()
Both assumptions desribe a strong stability property of the boundary layer system (7). If ![]() is assumed to be sufficiently close to
is assumed to be sufficiently close to ![]() , then assumption 2.3 encompasses assumption 2.2. We also note that the nonsingularity of
, then assumption 2.3 encompasses assumption 2.2. We also note that the nonsingularity of ![]() implies that the root
implies that the root ![]() is distinct as required by assumption 2.1. We have the following fundamental result, the so called “Tikhonov’s theorem”.
is distinct as required by assumption 2.1. We have the following fundamental result, the so called “Tikhonov’s theorem”.
Theorem 2.1: If assumptions 2.2 and 2.3 are satisfied, then the approximation (6), (8) is valid for all ![]() , and there exists
, and there exists ![]() such that (5) is valid for all
such that (5) is valid for all ![]() .
.
Under certain circumstances, the assumption 2.3 can be relaxed to
![]()
This relaxed form of assumption 3.2 can be used when dealing with optimal trajectories having boundary layers at both ends.
Now, consider the problem of finding a control ![]() that steers the state
that steers the state ![]() of the singularly perturbated system
of the singularly perturbated system
(10) ![]()
from ![]() ,
, ![]() to
to ![]() ,
, ![]() while minimizing the cost functional
while minimizing the cost functional
(11) ![]()
This problem can be simplified by neglecting ![]() in two ways. First, an optimality condition can be formulated for the exact problem and simplified setting
in two ways. First, an optimality condition can be formulated for the exact problem and simplified setting ![]() . The result will be a reduced optimality condition. Second, by neglecting
. The result will be a reduced optimality condition. Second, by neglecting ![]() in the system (10) the same type of optimality condition can be formulated for the reduced system. When the obtained optimality conditions are identical, it is said that the reduced system is formally correct. First, we formulate a necessary optimality condition for the exact problem, using the Lagrangian
in the system (10) the same type of optimality condition can be formulated for the reduced system. When the obtained optimality conditions are identical, it is said that the reduced system is formally correct. First, we formulate a necessary optimality condition for the exact problem, using the Lagrangian
![]()
where ![]() and
and ![]() are the adjoint variables associated with
are the adjoint variables associated with ![]() and
and ![]() respectively. The Lagrangian necessary condition
respectively. The Lagrangian necessary condition
(12) 
give
(13) 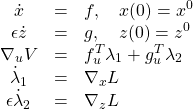
The reduced necessary condition is now obtained by setting ![]() in (13) and disregarding the requirement that
in (13) and disregarding the requirement that ![]() , which must be dropped because the second and fifth equation in (13)
, which must be dropped because the second and fifth equation in (13)
degenerate to
(14) ![]()
and are not free to satisfy arbitrary boundary conditions.
On the other hand, the reduced problem is obtained by setting ![]() in (10) and dropping the requirement that
in (10) and dropping the requirement that ![]() and
and ![]() , i.e. the reduced problem is defined as
, i.e. the reduced problem is defined as
(15) 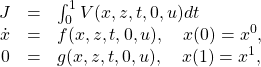
Applying the Lagrangian necessary condition to this problem, we arrive at
(16) 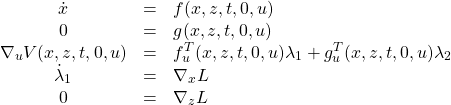
subject to ![]() ,
, ![]() . By setting
. By setting ![]() in (13), and comparing the result with (16), we come to the following conclusion.
in (13), and comparing the result with (16), we come to the following conclusion.
Lemma 2.1: The reduced problem (15) is formally correct.
Using the Hamiltonian form of (15), we define
![]()
and we get the equations
(17) 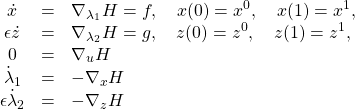
Note that we make use of ![]() rather than
rather than ![]() in the definition of
in the definition of ![]() . This means that the Hamiltonian adjoint variable associated with
. This means that the Hamiltonian adjoint variable associated with ![]() is
is ![]() . Applying the Hamiltonian condition to the problem
. Applying the Hamiltonian condition to the problem
(18) 
Using the Hamiltonian
![]()
we obtain
(19) 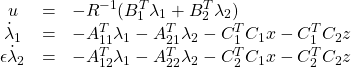
Substitution into (18) results in the boundary value problem
(20) 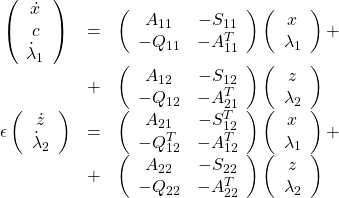
and the boundary conditions
![]()
where
![]()
and
![]()
Writing the system in a more compact form
(21) 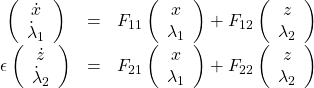
we see that this system is in the familiar singularly perturbated form. To define its reduced system, we need ![]() . However, anticipating that
. However, anticipating that ![]() will be the Hamiltonian matrix for a fast subsystem, we
will be the Hamiltonian matrix for a fast subsystem, we
make the following assumption.
Assumption 2.4: The eigenvalues of ![]() lie off the imaginary axis for all
lie off the imaginary axis for all ![]() , i.e. there exists a
, i.e. there exists a
constant ![]() such that
such that
![]()
Under this assumption ![]() exists and the reduced necessary condition is
exists and the reduced necessary condition is
(22) 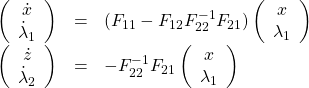
subject to ![]() . From lemma 2.1, we know that the same necessary condition is obtained by setting
. From lemma 2.1, we know that the same necessary condition is obtained by setting ![]() in (18), even if
in (18), even if ![]() does not exist.
does not exist.
Assumption 2.5: The solution of the reduced problem exists and is unique.
Theorem 2.2: Consider the time-invariant optimal control problem (18) where ![]() . If assumptions 2.4 and 2.5 hold and if
. If assumptions 2.4 and 2.5 hold and if
![]()
then there exists an ![]() such that for all
such that for all ![]() and all
and all ![]() the optimal trajectory
the optimal trajectory ![]() and the corresponding optimal control
and the corresponding optimal control ![]() satisfy
satisfy
(23) 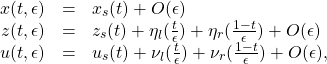
where ![]() ,
, ![]() ,
, ![]() is the optimal solution of the reduced problem (22), while
is the optimal solution of the reduced problem (22), while ![]() ,
, ![]() ,
, ![]() ,
, ![]() , are solutions to boundary layer systems. This theorem is simple to apply. First, solve the reduced problem (22). Next, we determine the initial and terminal conditions
, are solutions to boundary layer systems. This theorem is simple to apply. First, solve the reduced problem (22). Next, we determine the initial and terminal conditions ![]() and
and ![]() from (23) at
from (23) at ![]() and
and ![]() as
as
![]()
These values are the correctors of the discrepances in the boundary conditions for ![]() caused by the reduced solution
caused by the reduced solution ![]() .
.
Consider the cheap control problem
(24) 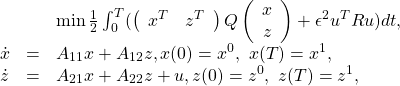
where ![]() is small. There is no loss of generality in considering the system in (24), because every linear system with a full-rank control input matrix can be represented in this form after a similarity transformation. Although the system in (24) is not singularly perturbated, a large
is small. There is no loss of generality in considering the system in (24), because every linear system with a full-rank control input matrix can be represented in this form after a similarity transformation. Although the system in (24) is not singularly perturbated, a large ![]() will force the
will force the ![]() -variable to act as a fast variable. The Hamiltonian function for this problem is
-variable to act as a fast variable. The Hamiltonian function for this problem is
(25) 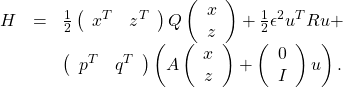
For ![]() and
and ![]() , the optimal control is
, the optimal control is
(26) ![]()
Now we rescale the adjoint variable ![]() as
as ![]() , transferring the singularity at
, transferring the singularity at ![]() from the functional to the dynamics, and write the adjoint equations in the form
from the functional to the dynamics, and write the adjoint equations in the form
(27) ![]()
Combining (24), (26) and (27), we obtain the singularly perturbated boundary value problem
(28) 
which is a special case of the problem (20). If ![]() , assumption 2.4 and 2.5 are satisfied, and we can set
, assumption 2.4 and 2.5 are satisfied, and we can set ![]() in (28) to obtain
in (28) to obtain
(29) ![]()
Substituting (29) into (28) gives the reduced slow system
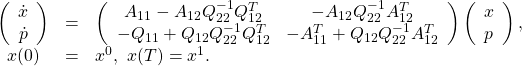
A cheap control problem where ![]() , results in a problem which is easier to solve because the corresponding Riccati equation is algebraic, but we must require the existence of a unique positive semidefinite solution to that Riccati equation, which stabilizes the system.
, results in a problem which is easier to solve because the corresponding Riccati equation is algebraic, but we must require the existence of a unique positive semidefinite solution to that Riccati equation, which stabilizes the system.
Thus, consider the functional to be minimized
(30) ![]()
(31) ![]()
where ![]() is nonsingular,
is nonsingular, ![]() ,
, ![]() and
and ![]() is small. To regulate the output
is small. To regulate the output
![]()
we set ![]() . We will make the following assumptions.
. We will make the following assumptions.
Assumption 2.6: ![]() is a positive-definite matrix.
is a positive-definite matrix.
Under this assumption, a two-time-scale decomposition of the problem
is possible.
Assumption 2.7: The algebraic Riccati equation corresponding to the problem (30)-(31) has a unique positive semidefinite stabilizing solution.
Under assumptions 2.6 and 2.7 we can apply theorem 2.2 to the problem (30)-(31) and approximate ![]() ,
, ![]() and
and ![]() by the expressions in (23), respectively.
by the expressions in (23), respectively.
