Consider the optimal control problem of minimizing the functional
(1) ![]()
(2) 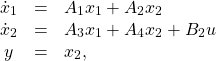
so that
![]()
We make the assumptions that the system (2) is time-invariant, has relative degree ![]() ,
, ![]() is stabilizable,
is stabilizable, ![]() is detectable and that
is detectable and that ![]() is nonsingular. (In lemma 3.1 below we show which systems can be represented in this form.) We want to study the limiting behavior of the solution to this problem, i.e. when the closed-loop system is stable, as
is nonsingular. (In lemma 3.1 below we show which systems can be represented in this form.) We want to study the limiting behavior of the solution to this problem, i.e. when the closed-loop system is stable, as ![]() tends to zero.
tends to zero.
We begin with a heuristic analysis of the problem of finding a feedback control law that minimizes the functional (1) and stabilizes the system. Since ![]() is nonsingular,
is nonsingular, ![]() is completely controllable. Thus, we can use
is completely controllable. Thus, we can use ![]() to control
to control ![]() . If
. If ![]() is bounded, the cost of control is small for small
is bounded, the cost of control is small for small ![]() .
.
Suppose that ![]() is stable. Then we see that
is stable. Then we see that ![]() minimizes the functional. In this case we can find a bounded feedback control which makes the output zero. Hence the remaining dynamics
minimizes the functional. In this case we can find a bounded feedback control which makes the output zero. Hence the remaining dynamics
![]()
are just the zero dynamics of the original system (see section 2.1), which are stable by assumption. On the other hand, if ![]() is antistable, stabilizability of the system implies that the pair
is antistable, stabilizability of the system implies that the pair ![]() is controllable. Since
is controllable. Since ![]() is completely controllable, we can let
is completely controllable, we can let ![]() be a control for
be a control for ![]() and find an optimal
and find an optimal ![]() by solving the reduced problem
by solving the reduced problem
(3) ![]()
(4) ![]()
The facts that ![]() is optimal and that
is optimal and that ![]() is a feedback control of the variable
is a feedback control of the variable ![]() suggest that the corresponding
suggest that the corresponding ![]() for the original problem (1)-(2) is optimal too. Unfortunately, since the system (4) is not detectable, an optimal solution to the reduced problem (3)-
for the original problem (1)-(2) is optimal too. Unfortunately, since the system (4) is not detectable, an optimal solution to the reduced problem (3)-
(4) may not exist, see Wonham [2, p. 280]. However, it is easy to see that an optimal solution to the problem (3)-(4) does exist if we make the assumption that ![]() has no eigenvalues on the imaginary axis. Nevertheless, we will give a detailed description of the solution in the end of this section.
has no eigenvalues on the imaginary axis. Nevertheless, we will give a detailed description of the solution in the end of this section.
First, we motivate our analysis of this special case by stating the following lemma.
Lemma 3.1: Consider the ![]() -dimensional linear system
-dimensional linear system
(5) ![]()
and suppose that the system has relative degree ![]() . (It is also natural to assume that the input matrix
. (It is also natural to assume that the input matrix ![]() has
has
linearly independent columns.) Then the system (5) can always be transformed to the form (2)
Proof: We can always write
![]()
in the controllability canonical form (see e.g. Kwakernaak and Sivan [3, pp. 60-61]),
(6) ![]()
where ![]() ,
, ![]() and
and ![]() is a non-singular
is a non-singular ![]() matrix (since
matrix (since ![]() has full column rank). Furthermore, the pair
has full column rank). Furthermore, the pair ![]() is completely controllable. Partition
is completely controllable. Partition ![]() as
as
![]()
The condition that the system has relative degree ![]() implies that
implies that ![]() and, by assumption, that the system has equal number of inputs and outputs (see section 2.1). Thus,
and, by assumption, that the system has equal number of inputs and outputs (see section 2.1). Thus,
![]()
so that ![]() must be non-singular. Now we let
must be non-singular. Now we let
![]()
or
![]()
which, after substitution into (6), yields
(7) 
Renaming the parameters in (7) shows the statement.![]()
Solving the optimal control problem (1)-(2), we define the Hamiltonian function

where ![]() and
and ![]() satisfy the adjoint equations
satisfy the adjoint equations
(8) ![]()
Setting ![]() , we find that the optimal control law is
, we find that the optimal control law is
(9) ![]()
In order to study the behavior of the solution as ![]() goes to zero, we use singular perturbation methods (see section 2.2). We rescale the adjoint variable
goes to zero, we use singular perturbation methods (see section 2.2). We rescale the adjoint variable ![]() as
as ![]() , so that the adjoint equations (8) can be written
, so that the adjoint equations (8) can be written
(10) ![]()
Multiplying the second equation in (2) by ![]() and using (9) and (10), we
and using (9) and (10), we
obtain the singularly perturbated system
(11) 
Since ![]() is nonsingular, we see that the system clearly satisfies the conditions of theorem 2.2 if we assume that the resulting Riccati equation has a unique positive semidefinite stabilizing solution. Therefore we set
is nonsingular, we see that the system clearly satisfies the conditions of theorem 2.2 if we assume that the resulting Riccati equation has a unique positive semidefinite stabilizing solution. Therefore we set ![]() to obtain
to obtain
(12) 
(13) ![]()
Now there exists an invariant subspace such that
(14) ![]()
(15) ![]()
Substitution of (14) and (15) into (13) gives the reduced system
(16) ![]()
where P satisfies the Riccati equation
(17) ![]()
Referring to our heuristic solution, we show that the solution to the reduced problem (16)-(17) is exactly the solution to the problem
(18) ![]()
(19) ![]()
The Hamiltonian function for this problem is
![]()
where
![]()
The optimal control law is
![]()
Letting
![]()
and
![]()
we get the closed-loop system
![]()
where ![]() is the positive semidefinite solution (if it exists) to the Riccati equation
is the positive semidefinite solution (if it exists) to the Riccati equation
![]()
Thus, we have shown that the problem (1)-(2) reduces, as ![]() , to the reduced problem (18)-(19). Now we will turn to the question of existence and uniqueness of the solution to the reduced problem.
, to the reduced problem (18)-(19). Now we will turn to the question of existence and uniqueness of the solution to the reduced problem.
Proposition 3.1: Consider the Riccati equation (17). If the matrix ![]() does not have any eigenvalues
does not have any eigenvalues
on the imaginary axis, there exists a unique, positive semidefinite solution ![]() to the Riccati equation which stabilizes the system (16).
to the Riccati equation which stabilizes the system (16).
Proof: Note that the detectability condition of theorem 2.5 is not satisfied for the problem (18)-(19). Therefore, we consider the three possible cases where ![]() is stable (all eigenvalues of
is stable (all eigenvalues of ![]() lie in the open left-hand complex plane), antistable (all eigenvalues of
lie in the open left-hand complex plane), antistable (all eigenvalues of ![]() lie in the open right-hand complex plane – we assumed that
lie in the open right-hand complex plane – we assumed that ![]() does not have any eigenvalue on the imaginary axis), and when
does not have any eigenvalue on the imaginary axis), and when ![]() has some eigenvalues in the open left-hand complex plane and some eigenvalues in the open right-hand complex plane.
has some eigenvalues in the open left-hand complex plane and some eigenvalues in the open right-hand complex plane.
Case 1:
Suppose that ![]() . Then the Riccati equation (17) has the unique positive semidefinite solution
. Then the Riccati equation (17) has the unique positive semidefinite solution ![]() and (16) becomes
and (16) becomes
![]()
Remark:
We see that this is just the zero dynamics of the system. Using the method outlined in section 2.1 on the system (2)
(20) 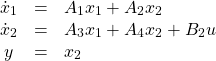
we set![]() , so that
, so that ![]() too. Then
too. Then
![]()
Since ![]() is nonsingular we choose
is nonsingular we choose
![]()
Changing coordinates according to
(21) ![]()
we obtain
(22) ![]()
Since ![]() , the zero dynamics of the system are described by
, the zero dynamics of the system are described by
![]()
Case 2:
Suppose that ![]() . Then
. Then ![]() must be controllable due to the stabilizability condition. Consider the Lyapunov equation
must be controllable due to the stabilizability condition. Consider the Lyapunov equation
(23) ![]()
By integrating the expression
![]()
using the Lyapunov equation (23), the stability of ![]() and the fact that
and the fact that ![]() , we see that
, we see that
![]()
is a solution. This is just the controllability Grammian of ![]() . (See e.g. Wonham [2,~pp.~277-278].) Furthermore, if
. (See e.g. Wonham [2,~pp.~277-278].) Furthermore, if ![]() is controllable, we have that
is controllable, we have that
![]()
is positive definite for every ![]() (see Wonham [2, p. 38]).
(see Wonham [2, p. 38]).
Thus ![]() is positive definite and therefore
is positive definite and therefore ![]() exists. If we let
exists. If we let ![]() and multiply the Lyapunov equation by
and multiply the Lyapunov equation by ![]() from the right and from the left, we see that this is just the reduced Riccati equation (17). Since
from the right and from the left, we see that this is just the reduced Riccati equation (17). Since ![]() is nonsingular, we have from (17)
is nonsingular, we have from (17)
![]()
so that (16) becomes
![]()
Since the transpose of a matrix has the same eigenvalues as the original matrix and the similarity transformation does not change the eigenvalues, the reduced system has the same eigenvalues as ![]() , but reflected in the imaginary axis.
, but reflected in the imaginary axis.
Writing the equation as
![]()
and referring to (13), we see that this is just the adjoint equation of ![]() .
.
Case 3:
Finally, suppose that ![]() is unstable with some stable and some unstable eigenvalues. Define the modal subspaces
is unstable with some stable and some unstable eigenvalues. Define the modal subspaces
(see Francis [4, pp. 85-86]) of ![]() as
as
(24) ![]()
where ![]() is the characteristic polynomial of
is the characteristic polynomial of ![]() . The factor
. The factor ![]() has all its zeros in Re
has all its zeros in Re ![]() and
and ![]() has all its zeros in Re
has all its zeros in Re ![]() . (There are no zeros on the imaginary axis.) It can be shown that
. (There are no zeros on the imaginary axis.) It can be shown that ![]() is spanned by the generalized real eigenvectors of
is spanned by the generalized real eigenvectors of ![]() corresponding to eigenvalues in
corresponding to eigenvalues in
Re ![]() and similarly for
and similarly for ![]() . These two modal subspaces are complementary, i.e. they are independent and their sum is all of
. These two modal subspaces are complementary, i.e. they are independent and their sum is all of ![]() . Thus
. Thus
![]()
Now, because ![]() is supposed not to have any eigenvalues on the imaginary axis, there exists a similarity transformation
is supposed not to have any eigenvalues on the imaginary axis, there exists a similarity transformation ![]() such that
such that ![]() has the form
has the form
![]()
where ![]() is stable and
is stable and ![]() is antistable. Partitioning
is antistable. Partitioning ![]() and
and ![]() accordingly, the algebraic Riccati equation (17) can then be written
accordingly, the algebraic Riccati equation (17) can then be written
(25) 
If we can find a positive semidefinite matrix ![]() which stabilizes the system (16), i.e. makes
which stabilizes the system (16), i.e. makes ![]() stable, and satisfies the Riccati equation (25),
stable, and satisfies the Riccati equation (25), ![]() must be unique. Suppose that
must be unique. Suppose that ![]() has the form
has the form
![]()
We see that we have the conditions
(26) ![]()
From case 1 and 2, we see that the Riccati equation (25) and the stability conditions (i) and (ii) are satisfied if we choose ![]() and
and ![]() as the positive semidefinite solution to the equation
as the positive semidefinite solution to the equation
(27) ![]()
Such a solution exists, since the pair ![]() is stabilizable by assumption. Thus, we have the resulting system
is stabilizable by assumption. Thus, we have the resulting system
(28) ![]()
It is easily seen that the closed-loop system is stable since its eigenvalues are exactly those of the stable matrix ![]() and those of the antistable matrix
and those of the antistable matrix ![]() with negative sign.
with negative sign.![]()
To interpret this result, first we observe that due to stabilizability, the unstable subspace must lie in the controllable subspace, ![]() , but we can not conclude that the intersection of the stable subspace and the
, but we can not conclude that the intersection of the stable subspace and the
controllable subspace is empty.
Consider the decomposition of case 3 into the stable and unstable modal subspaces. Suppose that ![]() , although this in general is not true. Then we simply have
, although this in general is not true. Then we simply have ![]() and we can put the system (19) in its controllability canonical form, i.e.
and we can put the system (19) in its controllability canonical form, i.e.
(29) ![]()
where the zeros in the matrices follow from ![]() and the
and the ![]() -invariance of
-invariance of ![]() . Therefore we have
. Therefore we have
(30) ![]()
which corresponds to ![]() in case 3. This would give the reduced system
in case 3. This would give the reduced system
(31) ![]()
Furthermore, we observe that ![]() , where
, where ![]() is the controllability Grammian. Thus, we can interpret the above results as follows:
is the controllability Grammian. Thus, we can interpret the above results as follows:
In the subspace ![]() , the optimal control gives the zero dynamics restricted to the stable subspace, in
, the optimal control gives the zero dynamics restricted to the stable subspace, in ![]() we have the adjoint equation subject to a similarity transformation by the inverse of the controllability Grammian of
we have the adjoint equation subject to a similarity transformation by the inverse of the controllability Grammian of ![]() , i.e. of
, i.e. of ![]() restricted to
restricted to ![]() . Finally, the subspace
. Finally, the subspace ![]() is naturally also affected by the minimum control which, however, does not change the stability properties of the matrix
is naturally also affected by the minimum control which, however, does not change the stability properties of the matrix ![]() .
.
To conclude, we observe that the conditions for ![]() -bounding are satisfied. Considering the decomposition and lemma 2.2 of section 2.3 we see that
-bounding are satisfied. Considering the decomposition and lemma 2.2 of section 2.3 we see that
![]()
Furthermore, from the comment following theorem 2.4 and the fact that ![]() is square and has full rank, the condition that
is square and has full rank, the condition that ![]() has no zeros on the imaginary axis is exactly the condition that
has no zeros on the imaginary axis is exactly the condition that ![]() does not have any eigenvalues on the imaginary axis, since the eigenvalues of
does not have any eigenvalues on the imaginary axis, since the eigenvalues of ![]() are the transmission zeros of the system.
are the transmission zeros of the system.
